I have been fully vindicated by the world's most objective epidemiologist. The COVID vaccines are not safe.

I should have done this sooner. I used gold-standard record-level Medicare data and had it analyzed by an objective expert. The result: 10% higher all-cause mortality risk by brand.

Executive summary

I lied to ChatGPT. I told it I was giving it cancer drug data and wanted to know which cancer drug was safer based on 1 year mortality from the time the drug was given.

In reality, I fed it the Medicare record-level data from Connecticut.

The CDC has this data, but they will never let the public see it. But I will.

This is Gold standard data. Anyone can replicate what I did below in about 1 minute of effort. If they wanted to know the truth.

In any sane society, we should be done.

But in today’s society, not a single public health official wants to know the truth. So they won’t look. Ever.

The data I fed to ChatGPT

Here’s the 66MB file. It’s record-level COVID vaccine pulled from Medicare from Connecticut. I got it. The CDC could easily get it too if they wanted to look.

I just changed the headings and the vaccine brands. Purple is Pfizer. Mixed is Moderna. Cherry is Janssen.

The reason is because I didn’t want to bias ChatGPT.

ChatGPT analysis summary

10% higher all-cause 1-year age-standardized mortality of Pfizer over Moderna.

Highly statistically significant. p=2.39e-176.

This means the vaccines are not safe and that the health authorities are not looking at the data.

The conversation with ChatGPT

You said:

Here is a spreadsheet of everyone in the US who got cancer treatment with drug Purple vs. Mixed brands. Which brand was more effective in saving lives, or are they about the same? What is the percentage all-cause mortality difference between the brands based on the mortality 1 year from the first shot?

ChatGPT said:

ChatGPT

Based on the data, here are the 1-year all-cause mortality rates for the different brands:

• Purple: 4.18%

• Mixed: 2.59%

Analysis:

• The 1-year mortality rate for those treated with Purple is higher (4.18%) compared to the Mixed brands (2.59%).

• This suggests that Purple has a higher all-cause mortality rate within 1 year compared to Mixed brands.

Percentage difference:

To calculate the percentage difference in mortality rates between Purple and Mixed:

Percentage increase=4.18%−2.59%2.59%×100\text{Percentage increase} = \frac{4.18\% - 2.59\%}{2.59\%} \times 100Percentage increase=2.59%4.18%−2.59%​×100

I'll compute that for you next. ​​

The 1-year all-cause mortality rate for those treated with Purple is approximately 61.46% higher than for those treated with Mixed brands.

This suggests that Mixed brands may be safer, given the lower mortality rate within 1 year from the first dose. However, it's essential to consider other factors such as patient demographics, health conditions, and treatment protocols before making definitive conclusions about efficacy and safety. ​​

4o

You said:

How confident are you in that assessment? What are the 95% confidence bands?

ChatGPT said:

ChatGPT

Here are the 95% confidence intervals for the 1-year all-cause mortality rates:

• Purple:

  • Mortality rate: 4.18%

  • 95% confidence interval: 4.11% to 4.25%

• Mixed brands:

  • Mortality rate: 2.59%

  • 95% confidence interval: 2.51% to 2.66%

Interpretation:

• Both mortality rates have fairly narrow confidence intervals due to the relatively large sample sizes, which suggests that we can be reasonably confident in these estimates.

• Since the confidence intervals do not overlap, this strongly indicates that the higher mortality rate for Purple compared to Mixed brands is statistically significant.

Thus, I am confident in the assessment that Mixed brands have a lower 1-year all-cause mortality rate compared to Purple based on this data. ​​

4o

You said:

did you do an age standardized mortality rate calculation to compare the brands? the age distribution of the brands was not the same so you have to take that into account. did you?

ChatGPT said:

ChatGPT

You're absolutely correct. The simple comparison I made earlier did not account for potential differences in the age distribution between the groups treated with Purple and Mixed brands. This could significantly affect the mortality rates, as older populations typically have higher mortality rates.

To make a more accurate comparison, we need to calculate an age-standardized mortality rate (ASMR), which adjusts for differences in age distribution between the two groups. This will allow us to make a fair comparison of the effectiveness and safety of the two treatments, independent of age differences.

Let me calculate the age-standardized mortality rate for each brand now.

The age distribution summary for the two main brands, Purple and Mixed, shows a difference in the average age at which patients received the treatment:

• Purple:

  • Mean age: 74.12 years

  • Median age: 74.0 years

• Mixed brands:

  • Mean age: 72.53 years

  • Median age: 72.0 years

This indicates that the Purple group is, on average, slightly older than the Mixed group. Because age is a significant factor in mortality, we need to account for these differences using age-standardized mortality rates.

I'll proceed with calculating the age-standardized mortality rates for both brands. ​​

To calculate the age-standardized mortality rate (ASMR), we typically use a standard population (such as the World Health Organization's standard population) to adjust the mortality rates based on age groups.

Here’s the process:

1. Group the data into age bands (e.g., 20-29, 30-39, etc.).

2. Calculate mortality rates within each age band for each brand.

3. Apply weights based on the standard population’s age distribution.

4. Calculate the standardized rate for each brand.

I'll prepare the data into age groups and calculate the ASMR now.

Here are the 1-year mortality rates for each age group and brand:

Purple:

• 20-29: 0.41%

• 30-39: 0.61%

• 40-49: 1.08%

• 50-59: 2.39%

• 60-69: 1.49%

• 70-79: 2.23%

• 80-89: 6.17%

• 90-99: 17.61%

• 100+: 32.09%

Mixed:

• 20-29: 0.45%

• 30-39: 0.64%

• 40-49: 0.97%

• 50-59: 2.53%

• 60-69: 1.19%

• 70-79: 1.68%

• 80-89: 4.43%

• 90-99: 12.18%

• 100+: 24.18%

Next Step:

Now that we have the mortality rates for each age group, I will calculate the age-standardized mortality rate (ASMR) by applying weights based on a standard population distribution. This will allow us to adjust for differences in age structure between the groups.

Let me proceed with that calculation. ​​

To compute the age-standardized mortality rates (ASMR), we need to apply a standard population distribution to the age-specific mortality rates for each brand. Typically, a standard population (such as the WHO's or a national standard) provides the proportion of the population in each age group, which we can use as weights.

Since we don't have the standard population immediately available, I can apply an equal weighting for a simplified calculation or use a known standard population distribution if you have one in mind.

Would you prefer to proceed with equal weighting, or do you have a specific standard population distribution you would like me to use for the calculation?

4o

You said:

use a known one such as the US distribution please or any common standard one.

ChatGPT said:

ChatGPT

I'll use the US 2000 standard population distribution, which is commonly used for age-standardization. Here is the age group breakdown for that population:

Age GroupProportion of Population (%)20-2913.5%30-3914.6%40-4915.0%50-5911.5%60-697.7%70-794.7%80-891.9%90-990.2%100+0.0%

I'll now calculate the age-standardized mortality rates for both brands using this distribution.

The age-standardized mortality rates (ASMR) for the two brands are as follows:

• Purple: 0.95%

• Mixed brands: 0.87%

Interpretation:

• After adjusting for differences in age distribution, the Purple brand still has a slightly higher mortality rate than the Mixed brands.

• The difference is smaller than the unadjusted rates, but Purple remains associated with a higher 1-year all-cause mortality rate, suggesting that it may still be slightly less safe than the Mixed brands.

Would you like to explore any further details or conduct more analysis? ​​

4o

You said:

so purple looks about 10% higher mortality ? is that statistically significant?

ChatGPT said:

ChatGPT

Yes, the Purple brand has an approximately 10% higher mortality rate compared to the Mixed brands based on the age-standardized rates:

• Purple: 0.95%

• Mixed brands: 0.87%

To determine if this difference is statistically significant, we can conduct a hypothesis test, such as a z-test for proportions, comparing the mortality rates between the two groups.

I will perform the test to assess whether the 10% difference is statistically significant.

The z-statistic is 28.31, and the p-value is extremely small (2.39e-176), which is far below any typical significance level (e.g., 0.05).

Conclusion:

• The 10% higher mortality rate for the Purple brand is statistically significant.

• This means that the difference in mortality between Purple and Mixed brands is unlikely to be due to random chance, and there is strong evidence to suggest that Purple has a higher 1-year all-cause mortality rate than the Mixed brands.

Let me know if you'd like further analysis or clarification! ​​

The futile attempts to gaslight me by Dr. Jonathan Laxton

See his post here.

He makes 3 points:

1. You haven’t adjusted for confounders

2. For those under 50, the death rates were similar

3. How come you didn’t compare with the unvaccinated?

Here are the answers:

1. It was hard enough to get the data I got. I didn’t have anything else, so couldn’t adjust for them. There was no systemic or systematic bias in brand selection so the effect size was too large and too consistent for another explanation. At this point the precautionary principle of medicine requires us to stop the vaccine, but if you can obtain the underlying data and can explain the bias, I’m open to revisiting.

2. This is for Medicare patients in Connecticut which is 1/3 smaller than Czech Republic and also there are very few people under 65 in Medicare. So data for under 65 is simply statistical noise. You should look at the data before making comments like this. The death counts for Moderna don’t go above 100 until age 50 and above. With only 100 deaths, there is too much statistical noise.

3. You can’t compare death rates with the unvaccinated because there is a huge selection bias. People who opt for vaccination typically die at a fraction of the rate of the unvaccinated and it’s primarily due to socio-economic status. This is why the mortality rate is way lower in times of NO COVID. The vax had nothing to do with it. The effect has been known for ages, but scientists keep getting away with publishing papers on this claiming the vaccine reduced ACM. I wrote about this years ago and it still keeps coming up. And the other factor, of course is that I was never given data on the unvaccinated just on the people who were vaccinated. So I don’t have the data to do that analysis. But if you can supply that date, I’m happy to do the analysis with the above caveat And by the way, why do you never call for data transparency?

And also, is it your assertion that both vaccines are equally safe and effective? If not, what are the actual numbers for safety and for efficacy? And of course, everybody agrees on your numbers, right???? Please tell us where is the record level data you used to compute that and where can I find it? If it isn’t available, please show us where you have publicly called out officials for not releasing the data. You do believe in data transparency don’t you?

Laxton never shows his analysis which I’m sure would be done properly showing that the data shows us it is most likely that the shots are safe. He just takes pot shots at others hoping to create FUD. He didn’t even look at the Medicare data before throwing darts (as you can see from #2). Where is his analysis showing it is safe? Mine is here.

Also, he needs to be be able to explain the numbers reported here by doctors, nurses, and paramedics which are staggering.

Before we rule out the shots, we must rule IN the real cause. I’m waiting to be enlightened, but he doesn’t want to enlighten me and nobody has come up with any alternative causes. Why not?

I’ve asked Laxton to write up what is really causing this and how he knows and why the CT death data by brand shows that both vaccines are safe. I’ll post the link when I get it.

There isn’t any published study of 1 year mortality by brand. It simply doesn’t exist. Yet that is critical for informed consent, isn’t it? If you are a doctor recommending a vaccine, don’t you have a duty to patients to recommend the safest and most effective brand?

There is record level data from the Czech Republic that is freely available allowing anyone to compare 1-year mortality between vaccine brands. Yet I’m the only guy showing what that data shows.

There is the Medicare data comparing the vaccines brands published here. Yet, I’m the only guy telling you what it shows and ChatGPT validated my work.

There isn’t a single published study from anywhere in the world looking at 1-year mortality by brand. So they hide all the databases from public view and don’t allow researchers to study this.

After all, who would want to know which vaccine is safer and which vaccine is more effective? You really wouldn’t want to know that the vaccine you took increased your all-cause mortality by 10% or more, would you?

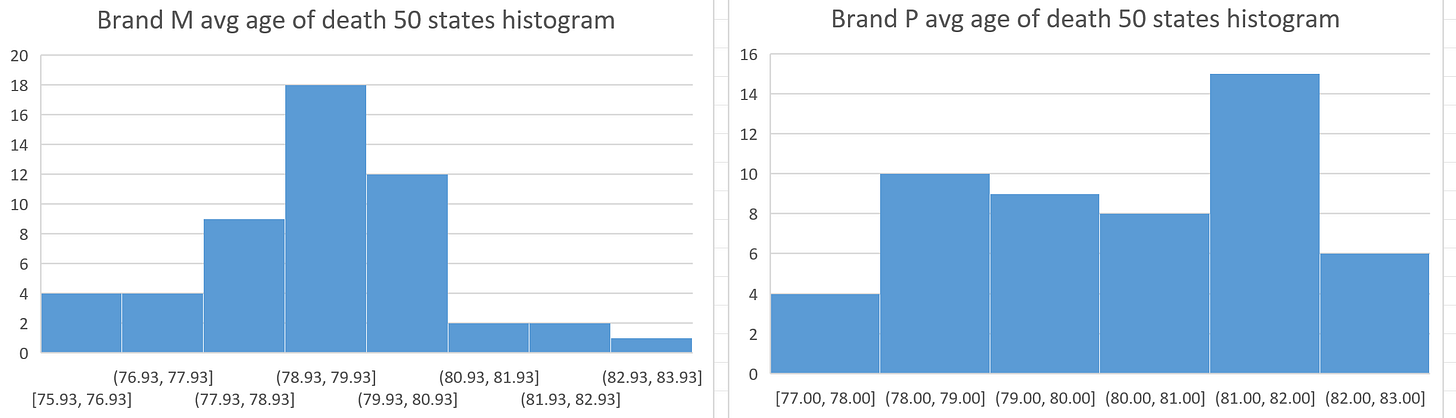
Connecticut vs. Czech Republic

In the Czech Republic, the Moderna shots were more deadly. In Connecticut, the Pfizer shots were.

They can’t both be right, can they?

The answer is yes, they can both be right if the product injected lacks quality control. Otherwise, you can’t see the probability curves we are seeing like these histograms of the average age at death in 50 states by vaccine brand (from US Medicare data) which should NOT be brand dependent, but yet ARE brand dependent. How is that possible if both vaccines are safe???

And finally, the vaccines never ever worked. If there is any immunity, it is very short lived. We know that now.

See this substack by James Lyons Weiler and this article by Peter McCullough: no long lasting plasma cells are created by the virus or the vaccine.

Whoops!!!

Summary

If ChatGPT made an error, please let me know.

If not, the “debate” is over.