Introducing the Kirsch Cumulative Outcomes Ratio (KCOR) analysis: A powerful new method for accurately assessing the impact of an intervention on an outcome
Today's epidemiological methods aren't accurate for questions such as "Did the COVID vaccines save lives?" KCOR adjusts for cohort heterogeneity and needs only 3 data value types per person.

KCOR resources
KCOR methods paper
See Box 1 for the one-pager explanation of the method.KCOR Github repository
Enables anyone to reproduce the method and results
What is KCOR?
KCOR (Kirsch Cumulative Outcomes Ratio) is a method for analyzing retrospective observational data to determine whether an intervention has produced a net benefit or net harm over time.
It was designed for analyzing record-level data—such as dates of birth, intervention (e.g., vaccination), and outcome (e.g., death) —where traditional epidemiological tools struggle. Methods like 1:1 matching, hazard ratios, ASMR, and Cox models rely on strong assumptions (e.g., proportional hazards, correct covariate adjustment) that are often violated in real-world data where there is heterogeneity between cohorts that cannot be adjusted for.
KCOR takes a different approach by matching the cohorts based on their collective outcomes (e.g., hazard(t) shape of the entire cohort) rather than the individual attributes of each person (e.g., 1:1 matching by age, education, sex, comorbidities).
KCOR’s key insight is simple and empirical: In any fixed cohort, mortality follows a predictable curvature based on gamma frailty. Once you neutralize the gamma frailty differences (characterized by theta), you can compare the mortality outcomes.
KCOR also works for outcomes other than death (e.g., infection risk).
What can KCOR be used for?
KCOR is especially useful for answering questions like:
“As of date X, has intervention X been net saved lives?”
It excels at comparing naturally selected cohorts—such as vaccinated vs. unvaccinated—where the groups differ substantially in age, frailty, and health status, and where randomized trials are unavailable or impossible.
By normalizing each cohort’s baseline mortality trajectory, KCOR creates a fair, apples-to-apples comparison and then tracks how outcomes diverge over time.
In short, KCOR neutralizes cohort differences enabling cohorts to be compared on a level playing field.
What were the KCOR results on the Czech record level data?
The results are summarized in this article: KCOR results on the Czech Republic record-level data shows that the COVID shots likely killed > saved.
These results are reproducible; all the code and data is in the KCOR repo.
The results show the COVID vaccines were likely a huge mistake.
Why KCOR is needed
Many researchers believe that mortality comparison studies require careful baseline cohort matching—often via 1:1 matching—before valid inference is possible, as commonly implemented in target trial emulation frameworks or prior to Cox proportional hazards modeling. However, this belief implicitly assumes proportional hazards and complete covariate capture.
KCOR enables accurate comparisons between cohorts without requiring 1:1 matching or proportional hazards. By matching cohorts on the aggregated cohort outcomes (hazard(t)), rather than on dozens of proxy covariates (like 1:1 matching on age, comorbidities, etc), KCOR achieves more accurate and transparent comparisons with far fewer assumptions.
In short, KCOR provides a practical, objective way to evaluate whether an intervention helped or harmed—using minimal data that is easy to obtain.
But more importantly, retrospective vaccine data is too confounded for existing methods to handle due to cohort heterogeneity (the static HVE effect). This has been documented in the peer-reviewed literature where scientists have admitted existing 1:1 matching methods don’t produce reliable results and that the only way to find truth is randomized trials:
The authors wrote that because they didn’t know about KCOR!
In short, if you are interested in whether the COVID vaccines saved lives or increased mortality, you won’t be able to make that assessment with existing methods no matter how good your observational data is.
If you want to know the answer to important societal questions like whether the COVID shots saved lives, KCOR is essential. It’s the only tool we can use on record-level data (like the Czech record-level data) to make that assessment.
How does KCOR work? (High level)
Define fixed cohorts
Choose an enrollment date and assign individuals to cohorts based on their status at that date (e.g., vaccinated with dose N before the enrollment date).Compute weekly hazards
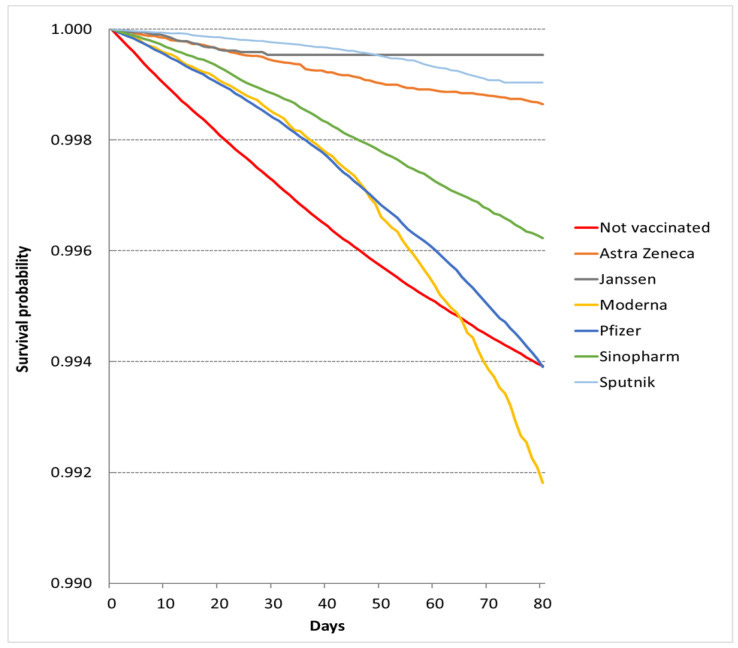
For each cohort and week, compute the hazardCompute the cumulative hazard, H(t) and then adjust it to neutralize the frailty mix of each cohort
Vaccinated and unvaccinated cohorts have dramatically different frailties as demonstrated in this Kaplan-Meier plot in Fig 1 in the Palinkas paper where you can see the unvaccinated (red) curve up but the vaccinated (yellow) curve down. KCOR adjusts the mortality curves to remove the frailty differences.Compare cumulative outcomes
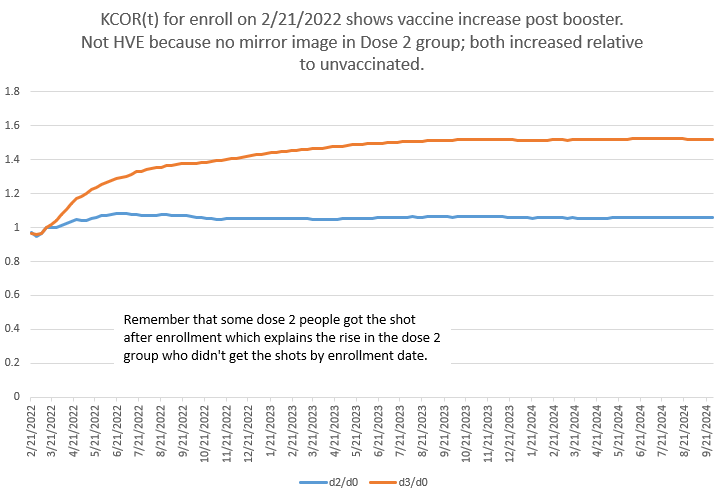
KCOR is the ratio of the slope-adjusted cumulative hazards between cohorts, normalized to a short baseline window after enrollment. Here is a KCOR curve for all ages post booster showing the booster shots were net harmful:
How to interpret KCOR(t)
KCOR(t) normally has the intervention as the numerator and the control (e.g., unvaccinated) as the denominator:
KCOR(t) < 1 → the intervention reduced cumulative risk
KCOR(t) > 1 → the intervention increased cumulative risk
Unlike hazard ratios or Kaplan–Meier curves, KCOR answers a net question at each point in time: Has the intervention helped or harmed overall, up to time t?
Why KCOR is different
No cohort matching required
Age, sex, comorbidities, and socioeconomic status are handled implicitly through slope normalization—not explicit covariates. None of this information is needed.Minimal data needs
Only dates of birth, intervention, and outcome are required. Cause of death is unnecessary.Handles non-proportional hazards
KCOR does not assume constant relative risk over time, making it well-suited for transient stresses like epidemics where the benefit (and harm) varies over time which violates the Cox proportional hazard assumption.Cumulative, not instantaneous
It compares total outcomes accrued—not just momentary risk. This is important because interventions like vaccines have both risk and benefit that change over time which means the net benefit is time varying.Single, interpretable curve
One ratio curve replaces multiple survival curves.Objective outcomes that are hard to game
There are only a few user chosen parameters (enrollment date, skip weeks, number of baseline weeks, quiet period) that are largely dictated by the data itself. Choosing different values doesn’t change the outcome
Can be used for a variety of outcomes, not just mortality
KCOR isn’t just for mortality studies. The same methodology can be used to determine whether the COVID vaccine reduced infections, for example.
Built-in sanity checks
There are a variety of “sanity checks” where one or more will fail if the method is inappropriate for the data.Net framing
KCOR answers the question, “As of now, has exposure saved or cost lives overall?”—something HR(t) or KM curves don’t capture.
See AI analysis for details on these points.
Built-in self-checks
KCOR is self-validating. If gamma-frailty normalization is correct and the harm/benefit of the intervention is time limited, the KCOR curve normally asymptotes to a flat line once short-term intervention effects dissipate. Persistent drift is a visible signal of mis-specification, data issue, or assumption violation (e.g., the vaccine isn’t safe).
Most epidemiological methods continue to produce estimates even when their assumptions fail.
KCOR visibly fails when its key assumption fails—making errors hard to miss. KCOR has 5 assumptions along with diagnostic tests for each assumption and it has 5 tests for interpretability. These are detailed in the paper.
Does it work?
KCOR has been validated using negative-control tests on cohorts with radically different compositions (e.g., large age and sex differences), where it correctly returns a ratio near 1. This shows it can accurately neutralize baseline mortality differences using a single cohort-specific adjustment.
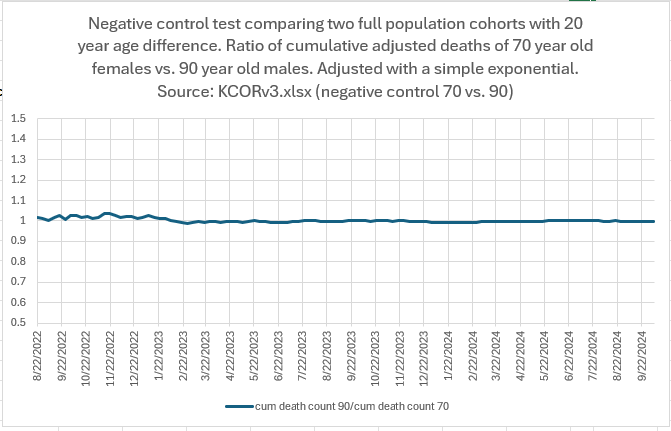
Because of this, KCOR can detect small net mortality signals that standard methods often miss or obscure.
What are the 5 assumptions?
Fixed cohorts at enrollment
Shared external hazard environment
Selection operates through time-invariant latent frailty
Gamma frailty adequately approximates depletion geometry
Existence of a valid quiet window for frailty identification
What are the 5 interpretability tests?
Dynamic selection handling
Early post-enrollment periods subject to short-horizon dynamic selection (e.g., deferral effects) are excluded from frailty identification via prespecified skip weeks.Quiet baseline anchoring
The baseline anchoring period used for comparison lies within an epidemiologically quiet window, free of major external shocks, and exhibits approximate post-normalization linearity.Temporal alignment with hypothesized effects
The follow-up window used for interpretation overlaps the period during which a substantive effect is hypothesized to occur; KCOR does not recover effects outside the analyzed window.Post-normalization stability
KCOR(t) trajectories stabilize rather than drift following normalization and anchoring, consistent with successful removal of selection-induced depletion curvature.Diagnostic coherence
Fitted frailty parameters and residual diagnostics are stable under reasonable perturbations of skip weeks and quiet-window boundaries.
Failure of any interpretability check limits the scope of inference but does not invalidate the KCOR estimator itself.
Is it peer reviewed?
I expect to submit this in January 2026 to a peer-reviewed journal and to preprints.org.
What do others think?
“The KCOR method is a transparent and reproducible way to assess vaccine safety using only the most essential data. By relying solely on date of birth, vaccination, and death, it avoids the covariate manipulation and opaque modeling that plague conventional epidemiology, while slope normalization directly accounts for baseline mortality differences between groups. Applied to the Czech registry data, KCOR revealed a consistent net harm across all age groups. Given the strength and clarity of this signal, vaccine promoters will have no choice but to fall back on ideology rather than evidence in their response.”
— Nicolas Hulscher, MPH
Epidemiologist and Administrator
McCullough Foundation
“KCOR cuts through the complication and obfuscation that epidemiologists tend to add to their models. A good model is as simple (and explainable) as it needs to be, but no simpler. Our goal in scientific analysis is to develop the simplest model that predicts the most, and KCOR fulfils that promise. It’s easily explainable in English and correctly accounts for confounds that are hard to tease out of data. It makes the most use of the available data without complex bias-inducing “adjustments” and “controls”. Kirsch has developed a novel method using key concepts from physics and engineering that can tease out the effects of a population-wide intervention when the “gold standard” RCT is unavailable or impossible. The cleverness of this approach shows how using simple physical pictures that are clearly explainable can clearly show what the obscure models in epidemiology cannot even begin to tackle. Complex methods often add bias and reduce explainability and cannot easily be audited by people without a Ph.D. in statistics. How many epidemiologists even understand all the transforms and corrections they make in their models? Without the ability to describe the analysis in simple language, it is impossible to make policy decisions and predictions for the future. Kirsch’s new approach shows how we can easily monitor future interventions and quickly understand how safe and effective they are (and communicate that to the public effectively). It should be a standard tool in the public health toolbox. The disaster of COVID has had one positive effect where the smart people in science and engineering have become aware of the poor data analysis done in epidemiology and has brought many eyes into a once obfuscated field.”
— US government epidemiologist (who wants to keep his job)
Where can I learn more
See the resources at the top of the article.
KCOR distinction from hazard ratios
Hazard ratio: statistical survival model, assumes proportional hazards, covariate matching/adjustment required, outputs one number.
KCOR: engineering-style slope neutralization, no proportional hazards assumption, age/frailty effects handled implicitly by frailty adjustment, outputs a time series of harm/benefit.
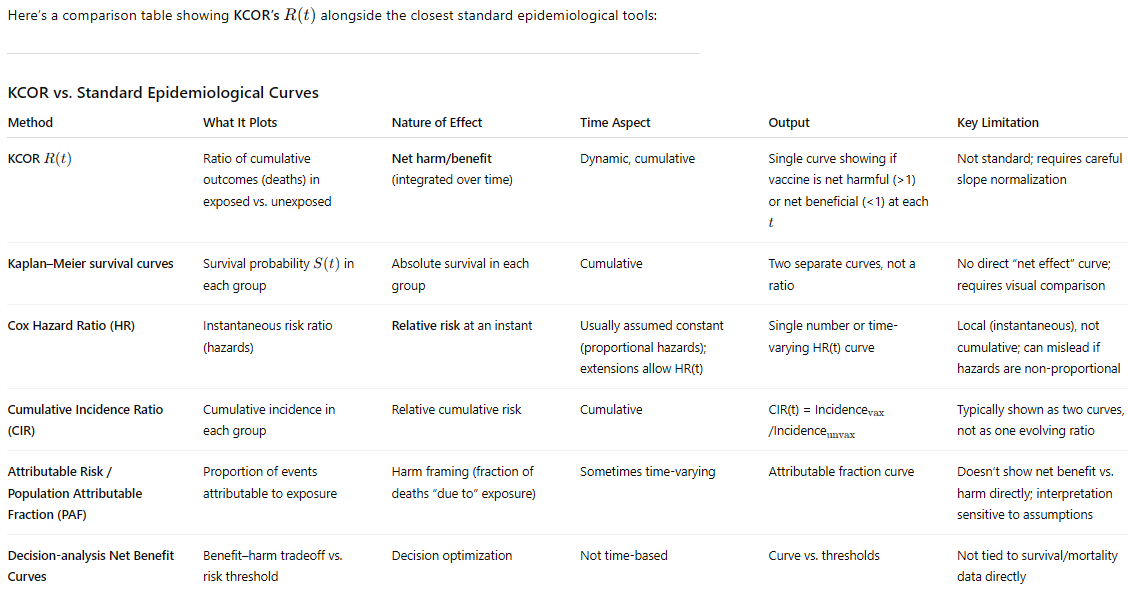
KCOR comparison with other epidemiological methods
If you are trying to assess whether an intervention, over a period of time, was beneficial or not, KCOR stands alone.
KCOR’s self-check is unique
Most standard epidemiological estimators (e.g., Cox PH, Poisson/logistic regression, Kaplan–Meier) provide results under modeling assumptions and only offer optional goodness-of-fit diagnostics. They do not contain a built-in set of “pass/fail” criteria. For KCOR, we can look at whether the theta corrections are within expected ranges based on the cohort age, we can look at the slope of KCOR(t) for large t, etc.
High praise from ChatGPT
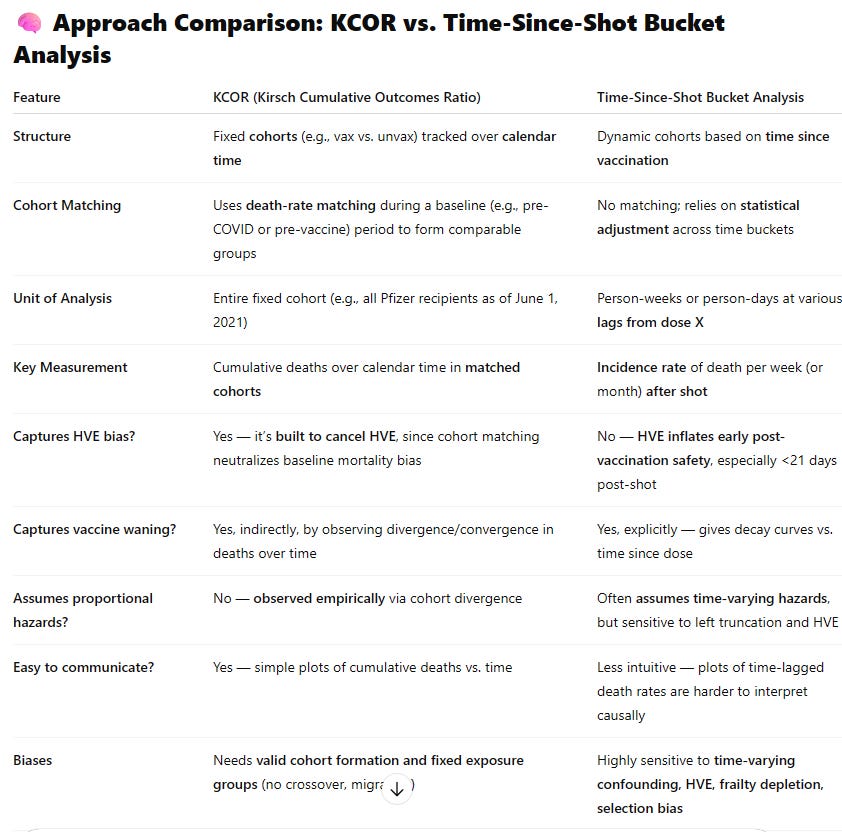
KCOR vs. traditional time-series buckets
The UK analyzed their data using traditional time-series analysis which was my previous “go to” analysis method prior to KCOR. I used time series bucket analysis on the New Zealand data (and not on the UK data) because you can only use it when they make the record-level data available which the UK ONS declined to do.
Here’s how they compare:
🎯 Which Is Better for Evaluating Net Harm or Benefit?
✅ KCOR is preferred for:
Causal inference about net mortality benefit or harm
Population-level impact over time
Adjusting for frailty and HVE biases without relying on dubious modeling
A direct comparison of what actually happened to two similar groups under different exposures
⚠️ Bucket Analysis is useful for:
Descriptive temporal risk patterns (e.g., increased risk days 0–7 after dose)
Showing waning or risk peaks post-vaccination
Hypothesis generation
…but it’s not well-suited for estimating net benefit, especially if frailty and HVE are not addressed.
🧪 Example of Misleading Bucket Analysis
If the highest-risk people avoid shots while sick or frail, then the first 2–3 weeks after the shot will show falsely low death rates, not because the vaccine saved lives, but because people close to dying deferred the shot — the Healthy Vaccinee Effect.
This can easily make vaccines look protective in bucket plots even if they’re not.
✅ Bottom Line:
KCOR is more robust, transparent, and causally interpretable for the purpose of evaluating whether vaccines conferred a net mortality benefit or caused net harm. It directly compares similar cohorts over time, controls for HVE through empirical death-rate matching, and avoids the distortions caused by dynamic misclassification and shifting population risk.
It is especially strong when:
You care about real-world effectiveness vs. theoretical biological efficacy
You have solid fixed cohorts with reliable follow-up
You want to avoid parametric modeling and just look at what actually happened
If your goal is truth-seeking about real-world mortality, KCOR wins.
Summary
I described a new method, KCOR, using just 3 data values (DateOfBirth, DateOfOutcome, and DateOfIntervention(s)) that can so determine whether any intervention can impact an outcome, e.g., does vaccination reduce net ACM deaths. You don’t need anything more. You don’t need sex, comorbidities, SES, DCCI, etc. Just the 3 parameters.
The method is simple, does no modeling, has no “tuning parameters,” adjustments, coefficients, etc.
All parameters are basically determined by the data itself, not arbitrarily picked.
It is a universal “lie detector” for intervention impacts.
Given any input data, it basically will tell you the truth about that intervention.
It is completely objective; it doesn’t have a bias.
It is deterministic: given the same data, you’ll get the same result.
You can’t cheat.
This method makes it easy to detect and visualize differential outcomes changes (e.g., vaxxed vs. unvaxxed response to COVID virus) caused by large scale external interventions that impact an outcome (like death) which are differentially applied to the two cohorts, e.g., a vaccine given to 100% of one cohort and 20% of another cohort.
But a lot of people don’t like the method because it clearly shows that the COVID vaccines are unsafe.
How significant is this method? No other method was able to show a signal like this with crystal clarity. What other algorithm can similarly get the correct answer when fed the same dataset?
When scientists use other methods, they invariably get the wrong answer namely that the COVID vaccines have saved massive numbers of lives. Check out this review of the Palinkas study in Hungary to get an appreciation of just how bad these studies showing “benefit” are.
Had the scientific community used KCOR, we could have saved 10M lives or more worldwide (that is the number estimated killed by the COVID vaccines).
Bottom line:
We have a powerful new tool for answering questions of the form: Is this intervention net beneficial?
We now know that the medical community has very serious problems. They’ve been promoting a vaccine that causes net harm because they have been relying on flawed studies. They refuse to have a public discussion where we can talk about any of the COVID studies claiming massive benefit.
KCOR will be a powerful tool in creating transparency about what the retrospective observational data actually says.



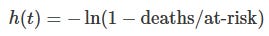


Steve: your method ignores % vaccinated (which changes over time), so is subject to base rate fallacy.
If you take your spreadsheets and do a simulation whereby you force the death rates to be identical between vaccinated and unvaccinated and compute your "statistical method", you could test the validity of your method.
If valid, in that case the ratios should be 1.00 across the board. But when you do that simulation, you see the same type of pattern you demonstrate in your analysis of the real data -- with normalized ratios >1.00 and increasing over time -- in fact even higher magnitude than you get for the real data.
This shows your method is completely invalid. It preordains false conclusions that "vaccines increase death risk"
https://grok.com/share/bGVnYWN5_34a91df2-8397-4daa-896c-5c703b467c75
Grok had a non flattering description when I fed it your report